Family Practice 215 Toll Gate Rd Warwick, Ri
Unlike linear information structures (Array, Linked List, Queues, Stacks, etc) which have only one logical style to traverse them, copse can exist traversed in different ways. Post-obit are the generally used ways for traversing trees.
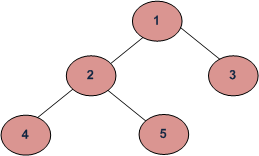
Depth First Traversals:
(a) Inorder (Left, Root, Right) : 4 ii 5 1 3
(b) Preorder (Root, Left, Correct) : i ii 4 v 3
(c) Postorder (Left, Right, Root) : iv five ii 3 ane
Breadth-Commencement or Level Gild Traversal: one two 3 four v
Please run across this post for Latitude-Beginning Traversal.
Inorder Traversal ( Practice ):
Algorithm Inorder(tree) one. Traverse the left subtree, i.due east., call Inorder(left-subtree) ii. Visit the root. 3. Traverse the right subtree, i.e., telephone call Inorder(right-subtree)
Uses of Inorder
In the instance of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal s reversed can exist used.
Example: In guild traversal for the above-given effigy is four 2 five 1 iii.
Preorder Traversal ( Exercise ):
Algorithm Preorder(tree) 1. Visit the root. 2. Traverse the left subtree, i.e., call Preorder(left-subtree) three. Traverse the correct subtree, i.due east., call Preorder(correct-subtree)
Uses of Preorder
Preorder traversal is used to create a copy of the tree. Preorder traversal is also used to get prefix expression on an expression tree. Delight encounter http://en.wikipedia.org/wiki/Polish_notation know why prefix expressions are useful.
Example: Preorder traversal for the above-given figure is 1 2 4 5 3.
Postorder Traversal ( Exercise ):
Algorithm Postorder(tree) 1. Traverse the left subtree, i.e., call Postorder(left-subtree) 2. Traverse the right subtree, i.e., call Postorder(correct-subtree) three. Visit the root.
Uses of Postorder
Postorder traversal is used to delete the tree. Please see the question for the deletion of a tree for details. Postorder traversal is also useful to get the postfix expression of an expression tree. Delight see http://en.wikipedia.org/wiki/Reverse_Polish_notation for the usage of postfix expression.
Example: Postorder traversal for the higher up-given figure is 4 5 2 3 1.
C++
#include <iostream>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
Node* newNode( int information)
{
Node* temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void printPostorder( struct Node* node)
{
if (node == Goose egg)
return ;
printPostorder(node->left);
printPostorder(node->right);
cout << node->information << " " ;
}
void printInorder( struct Node* node)
{
if (node == Zippo)
render ;
printInorder(node->left);
cout << node->information << " " ;
printInorder(node->right);
}
void printPreorder( struct Node* node)
{
if (node == NULL)
render ;
cout << node->data << " " ;
printPreorder(node->left);
printPreorder(node->right);
}
int primary()
{
struct Node* root = newNode(i);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "\nPreorder traversal of binary tree is \n" ;
printPreorder(root);
cout << "\nInorder traversal of binary tree is \n" ;
printInorder(root);
cout << "\nPostorder traversal of binary tree is \n" ;
printPostorder(root);
return 0;
}
C
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node* left;
struct node* right;
};
struct node* newNode( int data)
{
struct node* node
= ( struct node*) malloc ( sizeof ( struct node));
node->data = data;
node->left = Nothing;
node->right = Cipher;
render (node);
}
void printPostorder( struct node* node)
{
if (node == Zippo)
render ;
printPostorder(node->left);
printPostorder(node->right);
printf ( "%d " , node->data);
}
void printInorder( struct node* node)
{
if (node == Nix)
return ;
printInorder(node->left);
printf ( "%d " , node->data);
printInorder(node->right);
}
void printPreorder( struct node* node)
{
if (node == Aught)
render ;
printf ( "%d " , node->information);
printPreorder(node->left);
printPreorder(node->right);
}
int main()
{
struct node* root = newNode(i);
root->left = newNode(2);
root->right = newNode(three);
root->left->left = newNode(4);
root->left->right = newNode(five);
printf ( "\nPreorder traversal of binary tree is \n" );
printPreorder(root);
printf ( "\nInorder traversal of binary tree is \due north" );
printInorder(root);
printf ( "\nPostorder traversal of binary tree is \due north" );
printPostorder(root);
getchar ();
render 0;
}
Python
class Node:
def __init__( self , primal):
self .left = None
self .right = None
cocky .val = key
def printInorder(root):
if root:
printInorder(root.left)
impress (root.val),
printInorder(root.right)
def printPostorder(root):
if root:
printPostorder(root.left)
printPostorder(root.correct)
print (root.val),
def printPreorder(root):
if root:
impress (root.val),
printPreorder(root.left)
printPreorder(root.right)
root = Node( 1 )
root.left = Node( 2 )
root.right = Node( iii )
root.left.left = Node( 4 )
root.left.correct = Node( 5 )
print "Preorder traversal of binary tree is"
printPreorder(root)
print "\nInorder traversal of binary tree is"
printInorder(root)
print "\nPostorder traversal of binary tree is"
printPostorder(root)
Java
class Node {
int cardinal;
Node left, right;
public Node( int item)
{
central = item;
left = right = zippo ;
}
}
class BinaryTree {
Node root;
BinaryTree() { root = naught ; }
void printPostorder(Node node)
{
if (node == null )
return ;
printPostorder(node.left);
printPostorder(node.correct);
System.out.impress(node.fundamental + " " );
}
void printInorder(Node node)
{
if (node == null )
render ;
printInorder(node.left);
Organization.out.print(node.key + " " );
printInorder(node.right);
}
void printPreorder(Node node)
{
if (node == null )
return ;
System.out.print(node.key + " " );
printPreorder(node.left);
printPreorder(node.correct);
}
void printPostorder() { printPostorder(root); }
void printInorder() { printInorder(root); }
void printPreorder() { printPreorder(root); }
public static void chief(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node( ane );
tree.root.left = new Node( 2 );
tree.root.right = new Node( three );
tree.root.left.left = new Node( four );
tree.root.left.right = new Node( v );
System.out.println(
"Preorder traversal of binary tree is " );
tree.printPreorder();
System.out.println(
"\nInorder traversal of binary tree is " );
tree.printInorder();
System.out.println(
"\nPostorder traversal of binary tree is " );
tree.printPostorder();
}
}
C#
using System;
class Node {
public int key;
public Node left, right;
public Node( int item)
{
key = item;
left = right = null ;
}
}
class BinaryTree {
Node root;
BinaryTree() { root = nil ; }
void printPostorder(Node node)
{
if (node == null )
render ;
printPostorder(node.left);
printPostorder(node.right);
Console.Write(node.primal + " " );
}
void printInorder(Node node)
{
if (node == nil )
return ;
printInorder(node.left);
Console.Write(node.key + " " );
printInorder(node.right);
}
void printPreorder(Node node)
{
if (node == null )
return ;
Console.Write(node.key + " " );
printPreorder(node.left);
printPreorder(node.right);
}
void printPostorder() { printPostorder(root); }
void printInorder() { printInorder(root); }
void printPreorder() { printPreorder(root); }
static public void Main(Cord[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(one);
tree.root.left = new Node(2);
tree.root.correct = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.correct = new Node(5);
Console.WriteLine( "Preorder traversal "
+ "of binary tree is " );
tree.printPreorder();
Panel.WriteLine( "\nInorder traversal "
+ "of binary tree is " );
tree.printInorder();
Console.WriteLine( "\nPostorder traversal "
+ "of binary tree is " );
tree.printPostorder();
}
}
Javascript
<script>
class Node {
constructor(val) {
this .key = val;
this .left = naught ;
this .correct = null ;
}
}
var root = nix ;
function printPostorder(node) {
if (node == naught )
return ;
printPostorder(node.left);
printPostorder(node.right);
certificate.write(node.central + " " );
}
role printInorder(node) {
if (node == cipher )
return ;
printInorder(node.left);
document.write(node.cardinal + " " );
printInorder(node.right);
}
function printPreorder(node) {
if (node == null )
render ;
document.write(node.primal + " " );
printPreorder(node.left);
printPreorder(node.right);
}
root = new Node(1);
root.left = new Node(2);
root.correct = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
document.write( "Preorder traversal of binary tree is <br/>" );
printPreorder(root);
document.write( "<br/>Inorder traversal of binary tree is <br/>" );
printInorder(root);
document.write( "<br/>Postorder traversal of binary tree is <br/>" );
printPostorder(root);
</script>
Output:
Preorder traversal of binary tree is ane 2 4 5 3 Inorder traversal of binary tree is iv 2 v 1 3 Postorder traversal of binary tree is iv 5 2 3 1
One more than example:

Time Complication: O(due north)
Allow us run into different corner cases.
Complexity office T(due north) — for all bug where tree traversal is involved — can exist defined as:
T(northward) = T(k) + T(north – k – 1) + c
Where k is the number of nodes on i side of the root and n-g-one on the other side.
Let'southward exercise an assay of boundary conditions
Case 1: Skewed tree (One of the subtrees is empty and another subtree is not-empty )
thou is 0 in this instance.
T(due north) = T(0) + T(n-1) + c
T(north) = 2T(0) + T(due north-2) + 2c
T(n) = 3T(0) + T(northward-three) + 3c
T(n) = 4T(0) + T(due north-iv) + 4c
…………………………………………
………………………………………….
T(n) = (north-1)T(0) + T(1) + (n-ane)c
T(northward) = nT(0) + (n)c
Value of T(0) will be some abiding say d. (traversing an empty tree volition take some constants time)
T(n) = n(c+d)
T(n) = Θ(n) (Theta of n)
Case two: Both left and right subtrees have an equal number of nodes.
T(n) = 2T(|_n/2_|) + c
This recursive part is in the standard form (T(n) = aT(due north/b) + (-)(n) ) for principal method http://en.wikipedia.org/wiki/Master_theorem. If we solve information technology past master method we get (-)(n)
Auxiliary Space: If we don't consider the size of the stack for function calls then O(i) otherwise O(h) where h is the summit of the tree.
The height of the skewed tree is n (no. of elements) so the worst space complication is O(northward) and elevation is (Log north) for the balanced tree so the all-time infinite complication is O(Log northward).
Source: https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/
0 Response to "Family Practice 215 Toll Gate Rd Warwick, Ri"
Post a Comment